Experimentelle Bestimmung des Radius von Stanton

Eine Arbeit von Prof. Dr. Albert Hyperion (alias SpielerBlau)
Redaktion: Chhris und Siruck

Zusammenfassung

Unter Anwendung des Strahlensatzes wird gezeigt, wie der Radius bzw. Durchmesser des Sterns Stanton experimentell, d.h. mit direkt in Star Citizen zugänglichen Entfernungen, auf einfache Weise bestimmt werden kann.

Einleitung

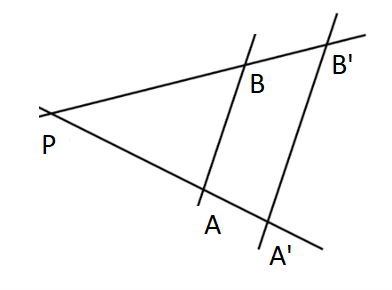
In der Elementargeometrie ist der Strahlensatz eine der wichtigsten Aussagen. Er befasst sich mit Streckenverhältnissen und ermöglicht es bei vielen geometrischen Überlegungen, Streckenverhältnisse zu berechnen. Anhand von Abb. 1 wird der zweite Strahlensatz illustriert.

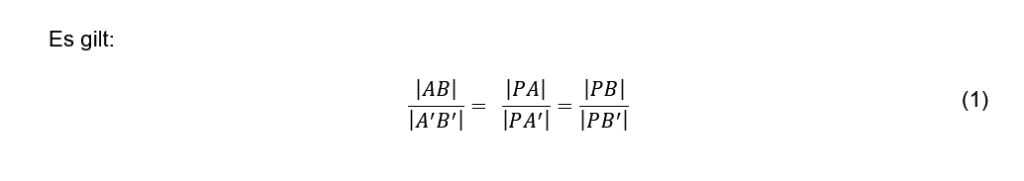
Abb. 1: Nach dem zweiten Strahlensatz verhalten sich die Abschnitte auf den Parallelen wie die ihnen entsprechenden, vom Scheitel aus gemessenen Strecken auf jeweils derselben Geraden. Dies ist in Gl. (1) formuliert.

Durchführung

Überträgt man den Satz Gl. (1) auf die in Abb. 2. dargestellte Situation unter Ausschluss von Beugungs- und Gravitationslinseneffekten, so ergibt sich die einfache Gleichung

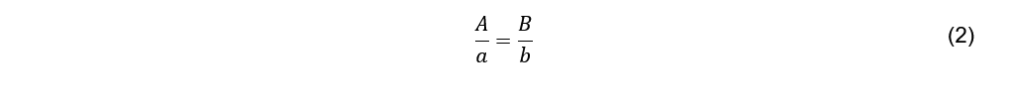
Umgestellt nach dem gesuchten Durchmesser Stantons folgt

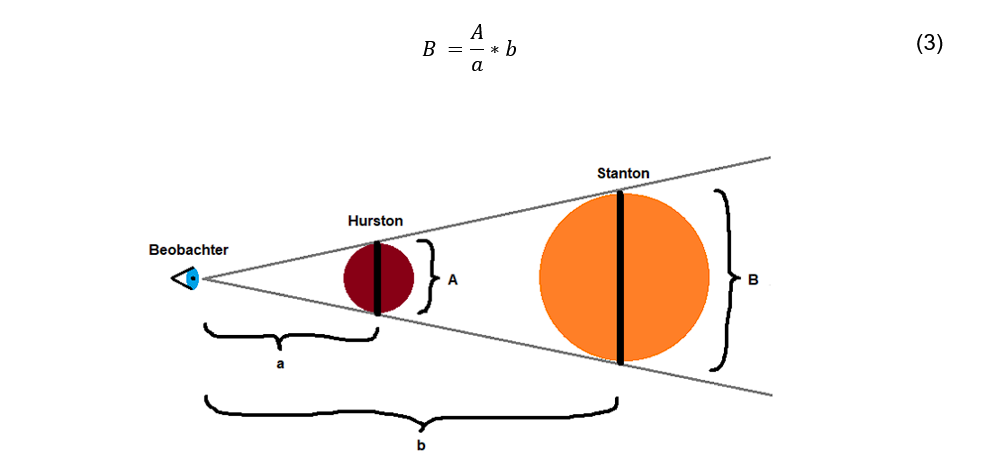
Abb. 2: Bedeckt ein Himmelskörper mit bekanntem Radius (bzw. Durchmesser) von einem Beobachtungspunkt aus exakt einen anderen Himmelskörper und können die Entfernungen vom Beobachtungspunkt zum ersten und zum zweiten Körper gemessen werden, kann man über den Strahlensatz Gl. (3) den Durchmesser des zweiten Himmelskörpers berechnen.

Wir haben früher schon den Radius (bzw. Durchmesser) von Hurston zu 1.000 km (bzw. 2.000 km) bestimmt. Für unsere jetzige Messung fliegen wir so weit von Hurston entgegen Stanton weg, bis wir an dem Punkt angelangt sind, an dem Hurston möglichst exakt Stanton abdeckt.

Abb. 3: Bilderserie des Fluges zum Punkt der Eklipse. Die Blickrichtung im Bild d) rechts entspricht genau der Blickrichtung im Schema Abb. 2.

Abb. 4: Großaufnahme der Sonnenfinsternis. Man beachte die sehr schön zu sehende Corona von Stanton.

Am Punkt der Eklipse lesen wir die Entfernung zu Hurston und Stanton im Mobiglas ab. Mit Hilfe von Gl. (3) berechnet sich der Durchmesser von Stanton somit wie folgt:

Ergebnis

Der Durchmesser von Stanton berechnet sich zu 1.299.966 km, also ca. 1,3 Mio. km. Der Radius von Stanton ist mit 650.000 km daher etwas kleiner als der Radius unserer Sonne (696.342 km).

Weitere Betrachtungen und Folgerungen

Da unsere Sonne und der Stern Stanton zu der gleichen Art Stern zählen (G-Stern), sollten auch die Dichten und Massen näherungsweise proportional sein. (Wegen der graduellen Dichteverteilung im Stern stimmt diese Annahme nicht exakt.)

Mit dem 0,93-fachen Radius (und damit dem 0,81-fachen Volumen bzw. Masse) für Stanton wird die Kepler-Konstante somit um das 1,23-fache größer. Nach den newtonschen Gravitationsgesetzen gilt:

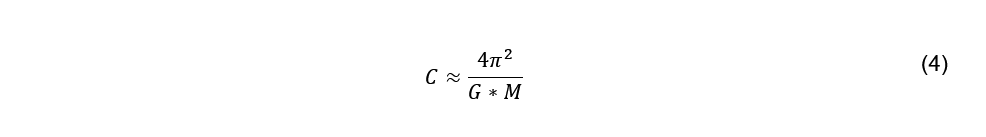
Darin ist C die Kepler-Konstante, G die Gravitationskonstante und M die Masse von Stanton. Mit dieser Näherung und unter Ausschluss relativistischer Effekte sowie mit dem dritten Keplerschen Gesetz nach Gl. (5), das besagt, dass das Verhältnis vom Quadrat der Umlaufzeit der Planeten und den Kuben der großen Halbachsen der Planetenbahnen konstant ist

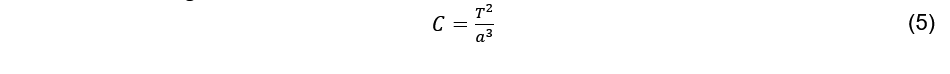
können die in Tab 1. aufgeführten astronomischen Daten für das Stantonsystem errechnet werden.

	Hurston	Crusader	ArcCorp	microTech	Reale Erde
Bahnradius [Mio. km]	12,85	19,15	30,37	57,15	149,6
Bahnumfang [Mio. km]	ca. 81	ca. 120	ca. 179	ca. 273	ca. 940
Umlaufzeit [in Erdentagen]	10,19	18,55	33,67	63,37	365,26
Bahngeschwindigkeit [km/s]	91,66	75,09	61,55	49,85	29,78
Eigenrotation in [h] = 1 Tag	2,5	6	3	4	24
Anzahl Tage Planet / Jahr	97,87	74,19	269,39	380,19	365,26

Tab. 1: Die unter Zuhilfenahme der Gleichungen (4) und (5) berechneten astronomischen Daten für das Stantonsystem

Ausblick

Die Vermessung eines Sternensystems, d.h. die Bestimmung relevanter astronomischer Größen, wie der Durchmesser stellarer Objekte, ihr Abstand zueinander, Umlaufbahnen und –zeiten, sowie zahlreicher daraus abgeleiteter Gesetzmäßigkeiten, wie zum Beispiel Tag-Nacht-Zyklen, partieller oder vollständiger Sonnenfinsternisse an gegebenen Orten des Systems usw., ist nicht nur für das Exploration Gameplay eine lohnende Unternehmung. Vielmehr ermöglichen die fundierten Kenntnisse dieser Zusammenhänge es uns oftmals erst, die notwendigen Vorbereitung für Unternehmungen ganz unterschiedlicher Art zu treffen. Dabei wollen wir natürlich nicht vergessen, dass Star Citizen ein Spiel ist und keine exakte Simulation des Universums.

Experimentelle-Bestimmung-des-Radius-von-Stanton Herunterladen