A work of Prof. Dr. Albert Hyperion (alias SpielerBlau)
Editing: Siruck and Chhris
Translator: Chhris
Abstract
Using the Ray Theorem, we show how the radius or diameter of the star Stanton can be
determined experimentally in a simple way, i.e. with distances directly accessible in Star Citizen.
Introduction
In elementary geometry, the ray theorem is one of the most important statements. It deals with
distance ratios and enables to calculate distances in many geometric considerations. The second
ray theorem is illustrated in Fig. 1.
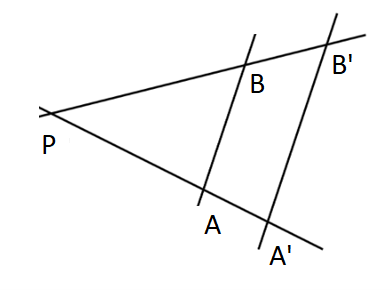
behave like their corresponding sections measured from the vertex on
the same straight line. This is formulated in Eq. (1)
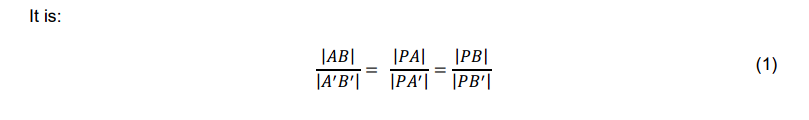
Realization
Applying the theorem Eq. (1) to the situation shown in Fig. 2. under exclusion of diffraction and
gravitational lensing effects, we obtain the simple equation
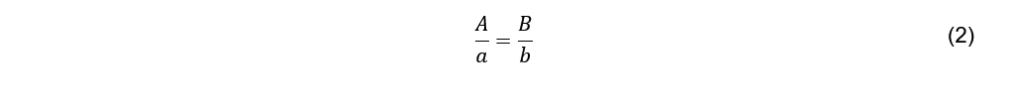
Rearrangement of Eq. (2) for the searched diameter B of Stanton results in
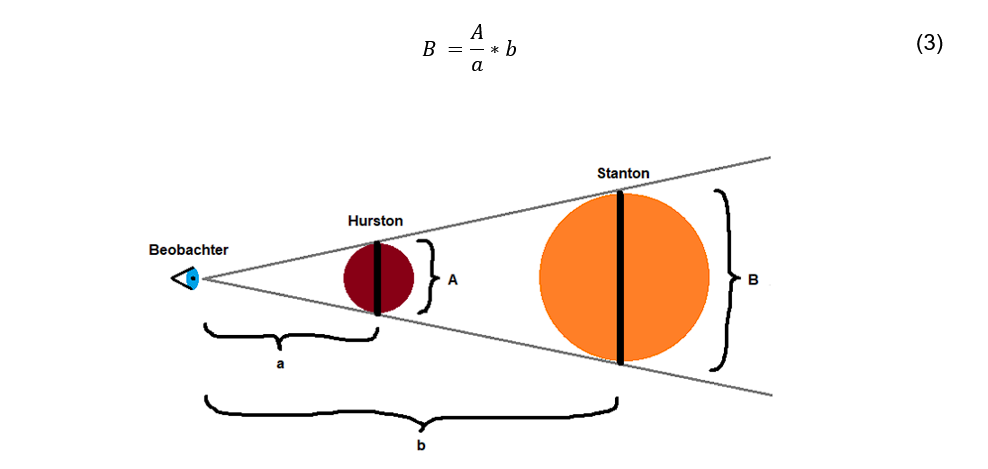
celestial body exactly from any observation point and if the distances from the
observation point to the first and to the second body can be measured, the
diameter of the second celestial body can be calculated using the ray theorem
Eq. (3).
We have determined the radius (or diameter) of Hurston to be 1,000 km (or 2,000 km) already
previously. For our present measurement, we fly as far away from Hurston towards Stanton until
we reach the point where Hurston covers Stanton as exactly as possible.

the viewing direction in the Fig. 2

visible corona of Stanton.
At the point of eclipse, we read the distance to Hurston and Stanton in the Mobi glass. Using Eq.
(3), the diameter of Stanton is then calculated as follows:

Result
The diameter of Stanton is calculated to be 1,299,966 km, or about 1.3 million km. Stanton’s
radius of 650,000 km is therefore somewhat smaller than the radius of our Sun (696,342 km).
Further considerations and conclusions
Since our sun and the star Stanton belong to the same kind of star (G-star), the densities and
masses should also be approximately proportional. (Because of the gradual density distribution
in the star this assumption is not exactly correct).
Therefore, with 0.93 times the radius (and thus 0.81 times the volume or mass) for Stanton,
Kepler’s constant becomes 1.23 times larger. According to Newton’s gravitation laws it is:
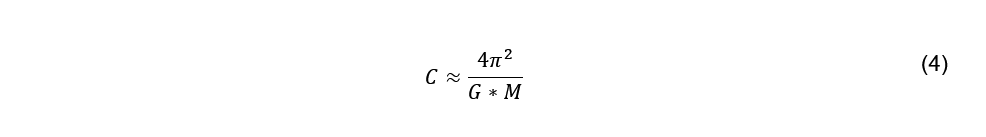
with C being Kepler’s constant, G the gravitational constant and M the mass of Stanton. With this
approximation and under exclusion of relativistic effects as well as with Kepler’s third law given in
Eq. (5), saying that the ratio of the square of the orbital period of the planets and the cubes of the
large semiaxes of the planetary orbits is a constant
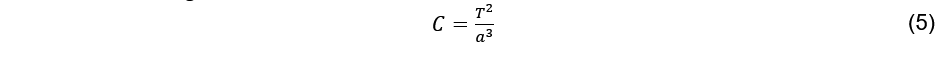
the astronomical data given in Tab 1. can be calculated for the Stanton system.
Tab. 1: Astronomical data calculated using equations (4) and (5) for the Stanton system.
| Hurston | Crusader | ArcCorp | microTech | Reale Erde | |
| Radius of planetary orbit [Mio. km] | 12,85 | 19,15 | 30,37 | 57,15 | 149,6 |
| Circumference of planetary orbit [Mio. km] | ca. 81 | ca. 120 | ca. 179 | ca. 273 | ca. 940 |
| Orbital period [in earth days] | 10,19 | 18,55 | 33,67 | 63,37 | 365,26 |
| Orbital velocity [km/s] | 91,66 | 75,09 | 61,55 | 49,85 | 29,78 |
| Self-Rotation in [h] = 1 planetary day | 2,5 | 6 | 3 | 4 | 24 |
| Number of planetary days per planetary year | 97,87 | 74,19 | 269,39 | 380,19 | 365,26 |
Outlook
The measurement of a star system, i.e. the determination of relevant astronomical quantities, such as the diameter of stellar objects, their distance to each other, their orbits and orbital times, as well as numerous conclusions derived from them, such as day-night cycles, partial or complete solar eclipses at given locations in the system, etc., is not only a rewarding enterprise for exploration gameplay. Rather, it is often the in-depth knowledge of such relationships that enables us to make the necessary preparations for undertakings of many different kinds. In doing so, of course, we don’t want to forget that Star Citizen is a game and not an exact simulation of the universe.





















2 Antworten zu “Experimental determination of the radius of Stanton”
Hat mit viel Spaß gemacht!
Ja, mir auch . .. .